贝塞尔曲线

贝塞尔曲线(Bezier Curve)的应用非常广泛, 比如CSS动画, Canvas以及PS中都有大量的应用.

介绍

贝塞尔曲线主要用于二维图形应用程序中的数学区下, 曲线由起始点, 终止点和控制点组成.

根据控制点的数量, 可以分为:

• 一阶贝塞尔曲线(2个控制点)
• 二阶贝塞尔曲线(3个控制点)
• 三阶贝塞尔曲线(4个控制点)
• N阶贝塞尔曲线(N+1个控制点)

绘制

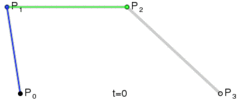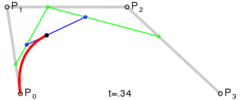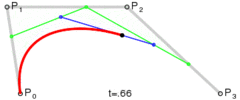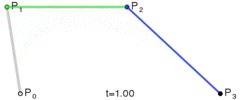
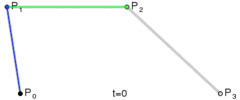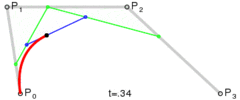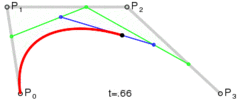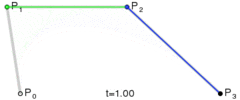
假定我们现在有一个三阶的贝塞尔曲线, 包含4个控制点, 分别为p0,p1,p2,p3.

绘制这个三阶贝塞尔曲线的基本步骤如下:

1. 四个控制点通过先后顺序进行连接, 形成了三条线段, 分别为p0p1,p1p2,p2p3. 然后通过一个参数t, 其中 t∈[0,1], 该参数表示线段上某个点距离起点的长度除以线段的长度. 比如p0p1上的一个点p0', 此时t的值就是p0p0'/p0p1, 其中p0'的位置如下所示:

2. 接下来对每一条线段做同样的操作, 得到三个控制点p0',p1',p2', 如下图所示:

3. 然后对这三个控制点重复第1步操作, 得出两个控制点p0'', p1'', 如下所示:

4. 最后使用同样的方法可以得到最后的一个点p0'''. 这个点就是贝塞尔曲线上的一个点.

通过控制t的值, 由0增加到1, 就绘制了一条由起点p0至终点p1的贝塞尔曲线.

求贝塞尔曲线上的点坐标

1. 一阶贝塞尔曲线

对于一阶贝塞尔曲线, 表现为就是一条直线.

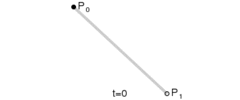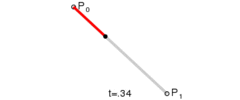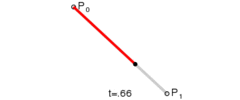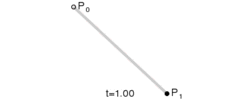
很容易根据t的值得出点的坐标:

$$B_1(t) = P_0 + (P_1 - P_0)t$$

然后可以得出:

$$B_1(t) = (1 - t)P_0 + tP_1, t \in [0,1]$$

2. 二阶贝塞尔曲线

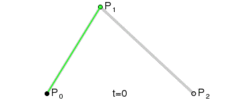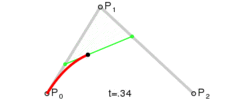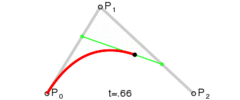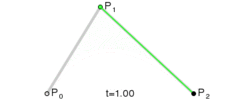
对于二阶贝塞尔曲线, 其实你可以理解为在$P_0P_1$上利用一阶公式求出点$P_0'$, 然后在$P_0P_1$上利用一阶公式求出点$P_1'$, 然后在$P_0'P_1'$上再利用一阶公式就可以求出最终贝塞尔曲线上的点$P_0''$. 具体推导过程如下:

• 先求出线段上的控制点:

$$P_0'=(1-t)P_0+tP_1$$

$$P_1'=(1-t)P_1+tP_2$$

• 将上面的公式带入公式中, 得出以下公式:

$$B_2(t)=(1-t)^2P_0+2t(1-t)P_1+t^2P_2, t \in [0, 1]$$

3. 三阶贝塞尔曲线

与二阶贝塞尔曲线类似, 可以通过相同的方法计算出下面的坐标公式:

$$B_3(t)=(1-t)^3P_0+3t(1-t)^2P_1+3t^2(1-t)P_2+t^3P_3, t \in [0,1]$$

4. 多阶贝塞尔曲线

n阶贝塞尔曲线的公式如下:

$$B(t)=\sum_{i=0}^nC_n^iP_i(1-t)^{n-i}t^i, t \in [0,1]$$

也就是:

$$B(t)=\sum_{i=0}^nP_ib_{i,n}(t), t \in [0,1]$$

其中的$C_n^i$的值为$\frac {n!} {(n-i)! \cdot i!}$, 其中$b_{i,n}(t)$:

$$b_{i,n}(t)=C_n^i(1-t)^{n-i}t^i, 其中i=0,1,...,n$$

CSS easing 属性的三阶贝塞尔曲线构造函数

CSS的easing贝塞尔曲线有一个特点, 它的起点和终点是固定[0,0],[1,1]的. 所以未知的点就只有两个, 也就是需要传入四个值, 并且这四个值的取值在[0,1]内.

所以创建一个类CubicBezier, 它拥有属性controlPoints:

class CubicBezier {
    constructor(x1, y1, x2, y2) {
        this.controlPoints = [x1, y1, x2, y2];
    }
}

通过上述代码初始化以后, 我们还需要根据t值获得坐标, 以及一个曲线上坐标集合的数据. 另外还需要使用三阶贝塞尔公式.

$$B_3(t)=(1-t)^3P_0+3t(1-t)^2P_1+3t^2(1-t)P_2+t^3P_3, t \in [0,1]$$

因为P_0点坐标[0, 0], $P_1$点坐标[1, 1]为所以公式进而可以写成:

$$B_{3,x}(t)=3t(1-t)^2x_1+3t^2(1-t)x_2+t^3, t \in [0, 1] \\ B_{3,y}(t)=3t(1-t)^2y_1+3t^2(1-t)y_2+t^3, t \in [0, 1]$$

class CubicBezier {
  constructor(x1, y1, x2, y2) {
    this.controlPoints = [x1, y1, x2, y2];
  }

  getCoord(t) {
    // 如果t取值不在0到1之间，则终止操作
    if (t > 1 || t < 0) return;
    const _t = 1 - t;
    const [ x1, y1, x2, y2 ] = this.controlPoints;
    const coefficient1 = 3 * t * Math.pow(_t, 2);
    const coefficient2 = 3 * _t * Math.pow(t, 2);
    const coefficient3 = Math.pow(t, 3);
    const px = coefficient1 * x1 + coefficient2 * x2 + coefficient3;
    const py = coefficient1 * y1 + coefficient2 * y2 + coefficient3;
    // 结果只保留三位有效数字
    return [parseFloat(px.toFixed(3)), parseFloat(py.toFixed(3))];
  }
}

利用该类, 我们就可以根据两个控制点构建Bezier示例, 通过这个示例我们可以根据t的值来获取点上的近似点.

这里使用了一个近似处理的办法, 具体如下:

1. 获取距离求值点最近的两个点
2. 通过这两个点可以得到一个直线方程
3. 最后将x轴坐标传入直线方程, 可以求得近似值.

因此, 进一步改造构造函数, 需要缓存固定数量坐标数组的属性coords, 以及获取coords的方法getCoordsArray, 最后还是获取y轴坐标的方法getY, 具体的实现方法如下:

class CubicBezier {
  constructor(x1, y1, x2, y2) {
    const precision = 100;
    this.controlPoints = [x1, y1, x2, y2];
    this.coords = this.getCoordsArray(precision);
  }
  
  getCoord(t) {
    // 如果t取值不在0到1之间，则终止操作
    if (t > 1 || t < 0) return;
    const _t = 1 - t;
    const [ x1, y1, x2, y2 ] = this.controlPoints;
    const coefficient1 = 3 * t * Math.pow(_t, 2);
    const coefficient2 = 3 * _t * Math.pow(t, 2);
    const coefficient3 = Math.pow(t, 3);
    const px = coefficient1 * x1 + coefficient2 * x2 + coefficient3;
    const py = coefficient1 * y1 + coefficient2 * y2 + coefficient3;
    // 结果只保留三位有效数字
    return [parseFloat(px.toFixed(3)), parseFloat(py.toFixed(3))];
  }
  
  getCoordsArray(precision) {
    const step = 1 / (precision + 1);
    const result = [];
    for (let t = 0; t <= precision + 1; t++) {
      result.push(this.getCoord(t * step));
    }
    this.coords = result;
    return result;
  }
  
  getY(x) {
    if (x >= 1) return 1;
    if (x <= 0) return 0;
    let startX = 0;
    for (let i = 0; i < this.coords.length; i++) {
      if (this.coords[i][0] >= x) {
        startX = i;
        break;
      }
    }
    const axis1 = this.coords[startX];
    const axis2 = this.coords[startX - 1];
    const k = (axis2[1] - axis1[1]) / (axis2[0] - axis1[0]);
    const b = axis1[1] - k * axis1[0];
    // 结果也只保留三位有效数字
    return parseFloat((k * x + b).toFixed(3));
  }
}

然后通过下述方式使用该类:

const cubicBezier = new CubicBezier(0.3, 0.1, 0.3, 1);
cubicBezier.getY(0.1); // 0.072
cubicBezier.getY(0.7); // 0.931

使用高阶贝塞尔曲线表示低阶贝塞尔曲线

一个n阶贝塞尔曲线可以通过一个形状完全一致的n+1阶的贝塞尔曲线表示, 由高阶贝塞尔曲线表示低阶贝塞尔曲线的过程, 我们称之为升阶.

我们需要$B(t)=(1-t)B(t) + tB(t)$这个公式:

1. 以二阶升三阶为例, 二阶贝塞尔曲线坐标公式为:

$$B(t)=(1-t)^2P_0+2t(1-t)P_1+t^2P_2$$

将等式带入:

$$P_0=(1-t)P_0 + tP_0 \\ P_1=(1-t)P_1 + tP_1 \\ P_2=(1-t)P_2 + tP_2 \\$$

然后可以得出:

2. 如果对于任意的n值, 我们该如何进行升阶, 公式如下:

整理来源

1. 深入理解贝塞尔曲线